Research
Uncertainty Quantification in Stochastic Systems
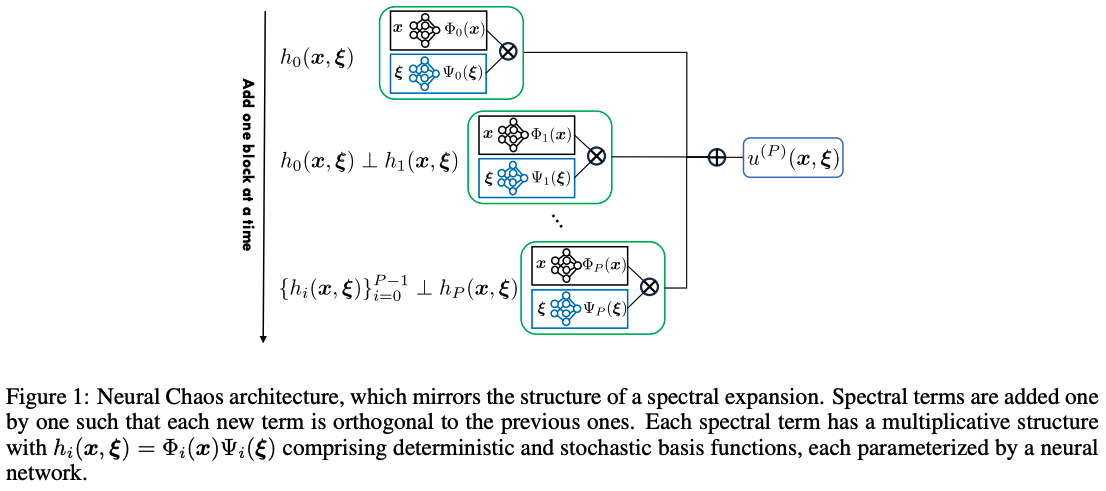
Neural Chaos is a neural-network-based formulation inspired by Polynomial Chaos Expansion (PCE) for modeling stochastic processes involving high-dimensional and statistically dependent inputs. While PCE is widely used in engineering applications, it may require special treatment when handling dependent random variables and can face scalability challenges due to its reliance on polynomial basis functions and tensor product structures. Neural Chaos, grounded in the same spectral representation formalism, replaces polynomial bases with neural-network–parameterized functions learned directly from data. Built on the RINO framework, it constructs basis functions that are orthogonal with respect to the underlying probability measure, enabling efficient spectral representations for uncertainty quantification in stochastic systems.
Relevant Publications:
- Neural Chaos: A Spectral Stochastic Neural Operator, B. Bahmani, et al., Journal of Computational Physics.
Operator Learning and Reduced Order Modeling
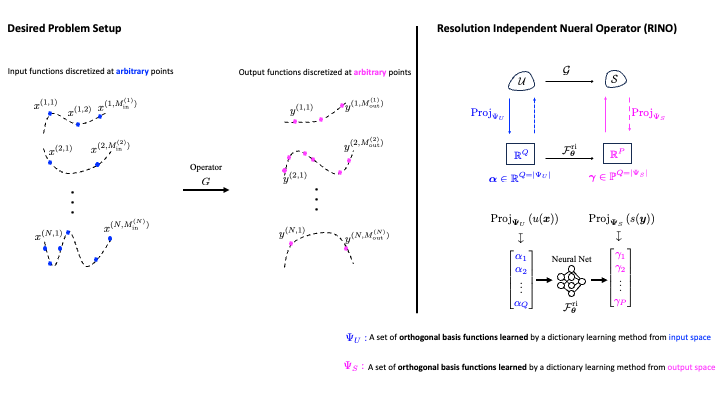
Most operator learning methods require input or output function spaces to be discretized on the same grid, limiting their applicability when data is defined on varying grids across realizations, such as in multiscale simulations. Our method, Resolution-Independent Neural Operator (RINO), addresses this by introducing a dictionary learning algorithm that extracts orthogonal, smooth basis functions from irregularly discretized data. These functions serve to project arbitrary discretized fields onto a finite-dimensional embedding space in which operator learning is conducted. This approach is interpretable from classical approximation theory and provides a natural error metric for detecting out-of-distribution samples.
Relevant Publications:
- A Resolution Independent Neural Operator, B. Bahmani, et al., Computer Methods in Applied Mechanics and Engineering.
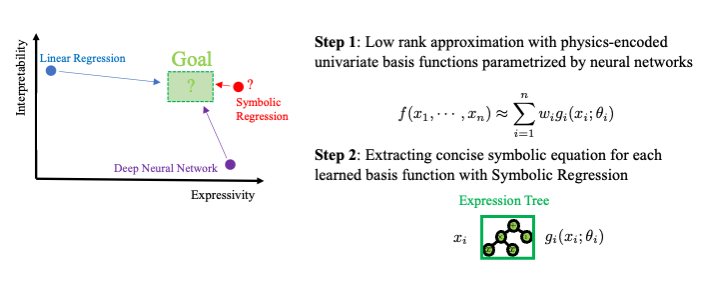
Interpretable Material Model Discovery with Machine Learning
Traditional constitutive models in mechanics rely on handcrafted equations rooted in phenomenological assumptions. While recent approaches using neural networks have enabled learning such models directly from data—experimental or computational—they often result in black-box or, at best, gray-box formulations, making it difficult to interpret how inputs (e.g., strains) are mapped to outputs (e.g., stress or strain energy). In this research, we introduce a scalable and interpretable framework that combines neural networks and symbolic regression for material model discovery. The key idea is a two-step decomposition of high-dimensional constitutive functions. First, we learn a low-rank representation by expressing the target function as an additive combination of univariate basis functions, each parameterized by a neural network. This step allows easy integration of physical constraints via differentiable programming. Second, we generate synthetic data from the learned basis functions and apply symbolic regression to extract concise, human-readable equations. The final constitutive model is assembled from these symbolic components, yielding interpretable and thermodynamically consistent formulations that reflect the kind of equations an expert mechanician might derive. We have demonstrated the effectiveness of this neural-symbolic scheme in discovering material models for a range of complex materials, including soft materials under large deformations, plastic yield surfaces of porous metals, granular materials, and others.
Relevant Publications:
- Physics-constrained Symbolic Model Discovery for Polyconvex Incompressible Hyperelastic Material, B. Bahmani and W. Sun, International Journal for Numerical Methods in Engineering.
- Discovering Interpretable Elastoplasticity Models via the Neural Polynomial Method enabled Symbolic Regression, B. Bahmani, et al., Computer Methods in Applied Mechanics and Engineering.
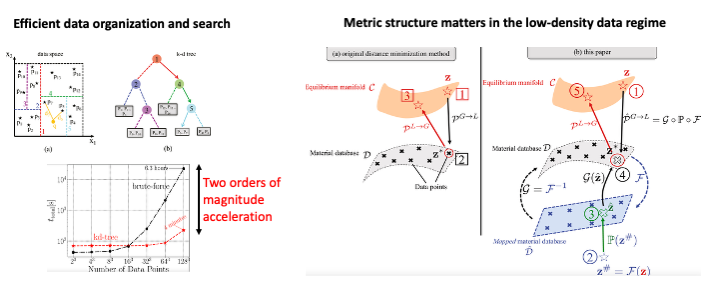
Manifold-Embedding Data-Driven Mechanics
Model-free distance-minimization methods provide a data-driven alternative to classical constitutive modeling by directly incorporating stress-strain data into field equations—without assuming an explicit stress-strain relationship. In this formulation, the governing equations become optimization problems that minimize the distance between material data and balance laws. Earlier approaches relied on energy-based Euclidean distances in phase space, which can misrepresent the geometry of nonlinear materials, especially with sparse or noisy data. To address this, we propose a new formulaiton that embeds the data into a latent space specifically constructed to admit a Euclidean structure. This enables the optimization to be performed via linear projection, reducing computational cost. The framework remains hybrid: local data searches can still be conducted within the latent space when needed. To better preserve the material data geometry, we design an isometric embedding that maintains local distances between data points before and after projection. This manifold-embedded approach offers a flexible continuum between model-based and model-free paradigms, adapting to the quality and availability of data. We extend the method to coupled multiphysics problems such as poroelasticity, introducing an additive distance metric over the joint phase space. This allows selective modeling—using data-driven approaches for some fields and traditional models for others. Finally, to ensure scalability, we develop a KD-tree–based spectral search algorithm tailored to the model-free setting, achieving orders-of-magnitude improvements in data retrieval efficiency.
Relevant Publications:
- Manifold embedding data-driven mechanics, B. Bahmani and W. Sun, Journal of Mechanics and Physics of Solids.
- Distance-preserving manifold de-noising for data-driven mechanics, B. Bahmani and W. Sun, Computer Methods in Applied Mechanics and Engineering.
- A kd-tree-accelerated hybrid data-driven/model-based approach for poroelasticity problems with multi-fidelity multi-physics data, B Bahmani and W. Sun, Computer Methods in Applied Mechanics and Engineering.
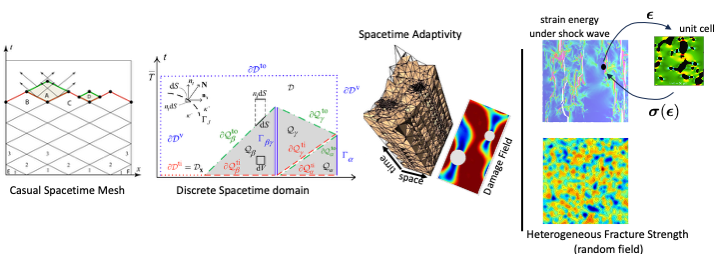
Stochastic Multiscale Fracture Modeling with Discontinuous Galerkin Method
To study the effect of material randomness, heterogeneity, and anisotropy on failure patterns in materials with complex microstructures subjected to high strain-rate loading, it is crucial to accurately model both fracture/damage phenomena and shock wave propagation—particularly in heterogeneous media. In this project, we develop methods based on the discontinuous Galerkin (DG) formulation, which, due to its fully discrete nature, is well-suited for problems involving discontinuities and wave propagation. While interfacial fracture models may offer a more accurate representation of fracture processes, they are computationally more demanding than continuum damage models. To improve computational efficiency—especially important for uncertainty propagation—we introduce a novel fully hyperbolic damage formulation within the spacetime discontinuous Galerkin framework. This formulation preserves the hyperbolic character of wave propagation phenomena, ensuring finite wave speeds. Furthermore, we propose a stochastic homogenization scheme that upscales relevant quantities of interest from microscale to macroscale in a statistically consistent manner.
Relevant Publications:
- Automated homogenization-based fracture analysis: Effects of SVE size and boundary condition, B. Bahmani, et al., Computer Methods in Applied Mechanics and Engineering.
- Asynchronous spacetime discontinuous Galerkin formulation for a hyperbolic time-delay bulk damage model, B. Bahmani and R. Abedi, Journal of Engineering Mechanics.
- A stochastic bulk damage model based on Mohr-Coulomb failure criterion for dynamic rock fracture, B. Bahmani, et al., Applied Sciences.
- Voronoi tessellation based statistical volume element characterization for use in fracture modeling, K. Acton, et al., Computer Methods in Applied Mechanics and Engineering.
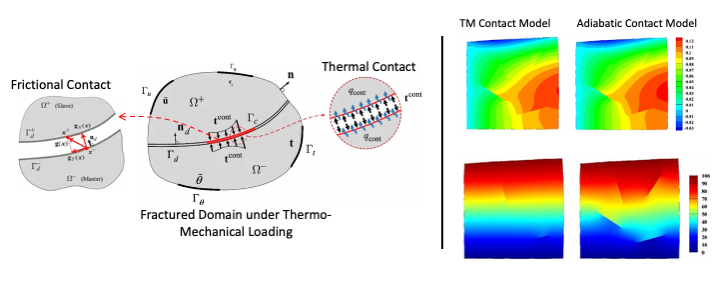
Multiphysics Contact Mechanics in Fractured Media with the Extended Finite Element Method
The eXtended Finite Element Method (XFEM) is a powerful numerical technique for solving partial differential equations with discontinuous solutions. By allowing the computational mesh to remain independent of discontinuities or sharp gradients, XFEM significantly simplifies mesh generation and interface tracking compared to standard FEM approaches. This makes it particularly effective for simulating fractured domains and contact mechanisms, where interfaces are implicitly represented using level set functions. In this work, we present a new XFEM-based formulation to model contact, bonding, and debonding phenomena across fracture surfaces under fully coupled thermo-mechanical loading. Specifically, we introduce an efficient algorithm to capture nonlinear interactions between mechanical and thermal fields at fracture interfaces. A key feature of our approach is the incorporation of pressure-dependent heat conduction across crack surfaces, enabling more accurate simulation of heat transfer in fractured materials.
Relevant Publications:
- Application of an enriched FEM technique in thermo-mechanical contact problems, A. Khoei and B. Bahmani, Computational Mechanics.